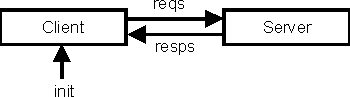
Lazy patterns are useful in contexts where infinite data structures are being defined recursively. For example, infinite lists are an excellent vehicle for writing simulation programs, and in this context the infinite lists are often called streams. Consider the simple case of simulating the interactions between a server process server and a client process client, where client sends a sequence of requests to server, and server replies to each request with some kind of response. This situation is shown pictorially in Figure 2. (Note that client also takes an initial message as argument.)
Let us further assume that the structure of the server and client look something like this:
client init (resp:resps) = init : client (next resp) resps
server (req:reqs) = process req : server reqs
where we assume that next is a function that, given a response from the server, determines the next request, and process is a function that processes a request from the client, returning an appropriate response.
Unfortunately, this program has a serious problem: it will not produce any output! The problem is that client, as used in the recursive setting of reqs and resps, attempts a match on the response list before it has submitted its first request! In other words, the pattern matching is being done "too early." One way to fix this is to redefine client as follows:
client init resps = init : client (next (head resps)) (tail resps)
Although workable, this solution does not read as well as that given earlier. A better solution is to use a lazy pattern:
client init ~(resp:resps) = init : client (next resp) resps
Because lazy patterns are irrefutable, the match will immediately succeed, allowing the initial request to be "submitted", in turn allowing the first response to be generated; the engine is now "primed", and the recursion takes care of the rest.